정의
입력 자료를 부분집합으로 분할(divide)하고, 각 부분집합에 대해서 정렬 작업을 완성(conquer)한 다음에 정렬된 부분집합들을 다시 결합(combine)하는 분할 정복(divide and conquer) 기법 중 하나로, 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식의 정렬 알고리즘
동작 방식 (2-way 병합, 오름차순 정렬 기준)
0. 일반적으로 정렬한 상태의 자료를 담기 위해 입력 자료의 크기만큼의 새로운 배열(리스트)을 선언해줌. 그러나 해당 포스팅에 기재한 소스코드는 정렬한 원소를 새로운 리스트에 담지 않고 입력값인 기존의 리스트를 재사용했음. 동작 방식에 대한 설명은 새로운 리스트를 선언했다고 가정한 채 진행.
1. 입력 자료를 두 개의 부분집합으로 분할하고, 각 부분집합을 계속해서 2개로 분할하는데 모든 부분집합의 원소가 1개일 때까지 분할
2. 총 2개의 원소를 가진 부분집합으로 만들기 위해 1개의 원소를 가진 부분집합들을 두 개씩 병합하는데, 병합 과정 중 아래의 흐름에 따라 정렬 진행
- 병합 대상인 두 부분집합 Left와 Right의 0번째 원소 대소 비교
- 더 작은 원소를 새로운 리스트에 삽입 (여기서는 Right[0]을 삽입했다고 가정)
- Right에서는 이미 하나의 원소가 삽입되었으므로 삽입된 원소는 지나치고 Left[0]과 Right[1] 대소 비교
- 위와 같은 과정을 반복하여 Left나 Right 둘 중 하나라도 모든 원소를 모두 삽입했을 경우 위 과정을 중단
- 아직 삽입하지 못한 원소가 남아있는 부분집합의 원소를 새로운 리스트에 순차적으로 삽입
3. 부분집합의 원소 개수가 2개, 4개, ... , n개(원래 입력 자료의 원소 개수)가 될 때까지 병합 과정 반복
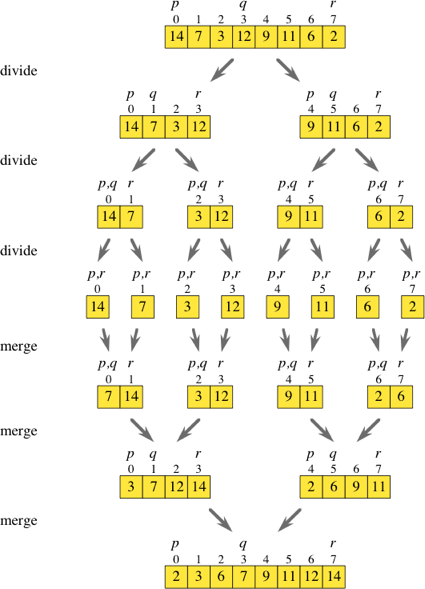
Pseudo Code도 없이 말로만 설명하는 것은 한계가 극명하다. 하여, Khan Academy에서 정리한 동작 방식 관련 사진 자료를 첨부하는 것이 좋겠다.
메모리 사용 공간
원소 n개에 대해서 2n개의 메모리 공간 사용
∵ 각 단계에서 병합하여 만든 부분집합을 저장할 공간 필요
연산 시간
1. 분할 단계 : n개의 원소를 분할하기 위해 log2 n번의 단계 수행
ex. 위 사진 자료를 보면, 8개의 원소를 가진 리스트를 3회(= log2 (8))에 걸쳐 1개의 원소를 가진 부분집합으로 분할
2. 병합 단계 : 부분집합의 원소를 비교하면서 병합하는 단계에서 최대 n번의 비교 연산 수행
ex. 위 사진 자료를 보면 총 15번 비교연산 수행
(1) 병합 1단계 : 14와 7 / 3과 12 / 9와 11 / 6과 2 --> 총 4번
(2) 병합 2단계 : 7과 3, 7과 12, 14와 12 / 2와 9, 9와 6 --> 총 5번
(3) 병합 3단계 : 3과 2, 3과 6, 7과 6, 7과 9, 12와 9, 12와 11 --> 총 6번
∴ 시간 복잡도 T(n) = O(N log N)
소스 코드
# 병합 정렬 (Merge Sort)
# 출처 : https://github.com/minsuk-heo/problemsolving/blob/master/sort/MergeSort.py
# 병합 정렬 - 오름차순 (Merge Sort - Ascending)
def mergeSort_ASC(arr):
if len(arr) > 1:
# 해당 조건문을 통해 자연스럽게 재귀함수의 탈출 조건 형성
mid = len(arr)//2
lefthalf = arr[:mid]
righthalf = arr[mid:]
mergeSort_ASC(lefthalf)
mergeSort_ASC(righthalf)
i=0
j=0
k=0
while i < len(lefthalf) and j < len(righthalf):
# 이걸 빠져나오는 순간 lefthalf, righthalf 둘 중 하나의 모든 원소는 다 쓴 것
if lefthalf[i] < righthalf[j]:
arr[k]=lefthalf[i]
i=i+1
else:
arr[k]=righthalf[j]
j=j+1
k=k+1
while i < len(lefthalf): # righthalf의 원소를 모두 썼을 경우
arr[k]=lefthalf[i]
i=i+1
k=k+1
while j < len(righthalf): # lefthalf의 원소를 모두 썼을 경우
arr[k]=righthalf[j]
j=j+1
k=k+1
def mergeSort_DESC(arr):
if len(arr) > 1:
# 해당 조건문을 통해 자연스럽게 재귀함수의 탈출 조건 형성
mid = len(arr)//2
lefthalf = arr[:mid]
righthalf = arr[mid:]
mergeSort(lefthalf)
mergeSort(righthalf)
i=0
j=0
k=0
while i < len(lefthalf) and j < len(righthalf):
# 이걸 빠져나오는 순간 lefthalf, righthalf 둘 중 하나의 모든 원소는 다 쓴 것
if lefthalf[i] > righthalf[j]:
arr[k]=lefthalf[i]
i=i+1
else:
arr[k]=righthalf[j]
j=j+1
k=k+1
while i < len(lefthalf): # righthalf의 원소를 모두 썼을 경우
arr[k]=lefthalf[i]
i=i+1
k=k+1
while j < len(righthalf): # lefthalf의 원소를 모두 썼을 경우
arr[k]=righthalf[j]
j=j+1
k=k+1
# 난수를 생성하여 test해보기 (Test by random number)
from random import randint
from random import randint
lst = [randint(1, 101) for i in range(8)]
print('Merge Sort(ASC) :', lst, end=' '); mergeSort_ASC(lst); print('->', lst)
# Merge Sort(ASC) : [1, 74, 61, 97, 11, 20, 40, 37] -> [1, 11, 20, 37, 40, 61, 74, 97]
lst = [randint(1, 101) for i in range(8)]
print('Merge Sort(DESC) :', lst, end=' '); mergeSort_DESC(lst); print('->', lst)
# Merge Sort(DESC) : [20, 61, 74, 14, 98, 49, 45, 31] -> [98, 74, 61, 49, 45, 31, 20, 14]작년에 알고리즘 강의를 수강할 때는 C로 짰기 때문에 Python으로는 어떻게 짜지 하며 고민을 많이 했다. 나동빈님의 강의와 소스코드를 기반으로 Python에 맞게 수정하고자 했으나, 그것보다는 허민석님의 강의와 소스코드를 참고하는 것이 좋다고 판단했다. 정말 깔끔하고 파이썬스럽다.
병합 정렬과 관련된 파이썬 코드가 별로 없었는데, 보통 C 계열의 언어로 코딩한 것을 보면 분할하는 함수 하나와 병합하는 함수 하나를 정의했고 분할하는 함수만 재귀 호출하는 형태이다. 또한 위 '동작 과정'에도 언급했지만 보통은 새로운 배열(리스트)을 추가적으로 선언한 후, 정렬되는 원소들을 그곳에 집어넣는 로직이다. 그런데 허민석님의 코드는 분할과 병합을 한 함수에 담아 재귀 호출하였고, 새로운 리스트를 선언하기보다는 입력값으로 주어지는 리스트를 계속 재활용하면서 공간 복잡도를 최소화하였다. 그래도 어쩔 수 없이 처음 분할할 때 lefthalf와 righthalf로 인해 공간 복잡도는 2n이겠지만, 나라면 생각도 못했을 코드다.
병합 정렬은 여태까지 포스팅했던 정렬 중 가장 성능이 좋은 정렬 방법이다. 아직 포스팅하지는 않았지만, (기수 정렬이나 카운팅 정렬 등과 같은 특이한 정렬을 제외하고) 평균적인 상황에서 가장 빠르다고 알려져 있는 퀵 정렬(Quick Sort)과도 평균 시간 복잡도가 동일하다. 물론 세심하게 따져보면 평균적인 상황에서는 퀵 정렬이 더 빠른 편이지만 말이다. 물론 추가적으로 n만큼의 공간을 요한다는 단점이 상당한 페널티로 작용할 때도 있다.
하지만 파이썬에 내장되어 있는 정렬 메서드는 최악의 경우 O(N^2)의 시간 복잡도를 가지는 퀵 정렬을 사용하지 않고, 병합 정렬과 삽입 정렬을 혼합한 개념의 Tim Sort(팀 정렬)을 사용한다. 결국 평균 시간 복잡도보다 최악의 경우의 시간 복잡도가 더욱 중요하다는 것을 방증하는 사례라고 생각한다.
이렇게 마지막 말을 쓰다 보니 추후에 정렬을 모두 포스팅한 후에는 각 정렬을 비교하며 정리하는 글을 하나 더 쓰는 것이 좋겠다는 생각이 든다.
'Dev > 알고리즘' 카테고리의 다른 글
| [알고리즘][파이썬/Python] 퀵 정렬 (Quick Sort) (2) | 2020.03.24 |
|---|---|
| [알고리즘][파이썬/Python] 쉘 정렬 (Shell Sort) (0) | 2020.03.22 |
| [알고리즘][파이썬/Python] 삽입 정렬 (Insertion Sort) (0) | 2020.03.21 |
| [알고리즘][파이썬/Python] 선택 정렬 (Selection Sort) (0) | 2020.03.20 |
| [알고리즘][파이썬/Python] 버블 정렬 (Bubble Sort) (0) | 2020.03.19 |
![[알고리즘][파이썬/Python] 병합 정렬 (Merge Sort)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbLtWzL%2FbtqDx6nKuOu%2FAAAAAAAAAAAAAAAAAAAAAAgqcB_RgvBATMOYHR7Z4cbliwUWceRWD-YloesOCvzu%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D5VwQgJgx3jb2ogTJRCngTFhoy%252FE%253D)