정의
기준 값을 중심으로 작은 원소들은 왼쪽 부분집합으로, 큰 원소들은 오른쪽 부분집합으로 분할하여 정렬하는 방식의 정렬 알고리즘
* 퀵 정렬도 분할과 정복(divide and conquer) 기법을 이용하는 정렬 알고리즘이다. 하지만 병합 정렬과 차이가 있는데, 병합 정렬이 분할 후 정복하는 원리였다면, 퀵 정렬은 정복 후 분할하는 원리의 정렬 알고리즘이다. 우선 기준 값보다 작은 원소들을 왼쪽 부분집합으로, 기준 값보다 큰 원소들은 오른쪽 부분집합으로 구분하는 정복 절차를 밟고, 기준 값을 중심으로 2개의 부분 집합으로 분할한다.
동작 방식
0. 기준 값을 보통 피벗(pivot)이라고 부르며, 선택하는 기준은 다양하겠으나 일반적으로 가장 왼쪽 원소를 피벗으로 지정한다. 본 글에서도 가장 왼쪽 원소를 피벗으로 지정할 것이다.
1. Left Index를 리스트의 가장 왼쪽에, Right Index를 리스트의 가장 오른쪽에 위치시킨다. (편의상 L와 R로 축약하여 설명)
2. L에 위치한 원소가 pivot보다 큰 값이 나올 때까지 L은 리스트의 오른쪽 방향으로 이동한다. 또한, R에 위치한 원소가 pivot보다 작거나 같은 값이 나올 때까지 리스트의 왼쪽 방향으로 이동한다.
3. L과 R이 교차하지 않았다면, 두 인덱스에 위치한 원소를 교환하고 다시 2번 과정으로 돌아간다.
* 이때 주의할 점은 L과 R이 가리키는 인덱스는 유지한 채, 두 인덱스에 위치한 원소만을 교환하는 것이다.
4. L과 R이 교차했다면, pivot과 R에 위치한 원소를 교환한다. 교환한 후의 pivot의 위치를 기준으로 왼쪽과 오른쪽 부분집합을 구분하고, 두 부분집합에 대해 퀵 정렬 알고리즘을 재귀 호출한다. 단, 새롭게 분할된 부분집합의 크기가 0이나 1일 경우 정렬할 필요가 없으므로 재귀 호출을 탈출하게끔 구현한다.
퀵 정렬은 아무래도 그림 없이는 이해하기가 많이 어려울 것 같아 오늘은 동작 방식을 그림으로 표현해봤다.

1. 우선 리스트의 가장 왼쪽에 있는 원소 '9'를 pivot으로 지정하며, 리스트의 가장 왼쪽 인덱스인 0을 L로, 가장 오른쪽 인덱스인 9를 R로 지정한다.
(사실 엄밀히 따진다면 L을 가장 왼쪽 인덱스인 0보다는 1로 설정하는 것이 아주 약간의 효율 증진에 도움이 된다. L은 pivot보다 큰 수가 발견되어야 멈추기 때문에 결코 0번 인덱스에서 멈출 수 없기 때문이다. 다만 더욱 직관적으로 이해하기 위해 L을 가장 왼쪽 인덱스인 0으로 위치시켰다.)
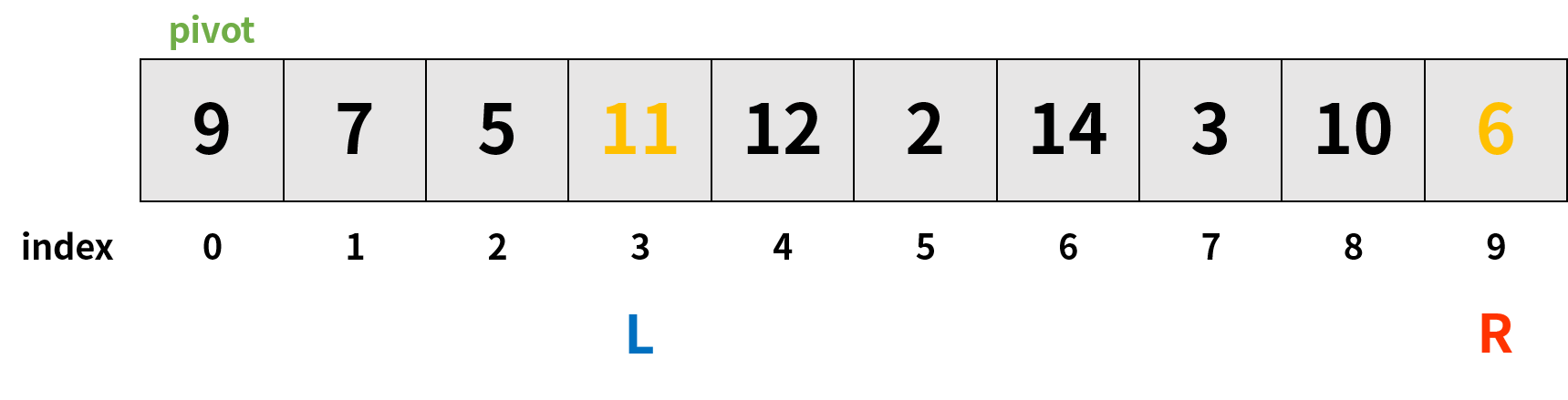
2. L은 L에 위치한 원소가 9(=pivot) 보다 큰 값이 나올 때까지 리스트의 오른쪽 방향으로 움직인다. 그에 따라 L은 오른쪽으로 움직이다가 3이라는 인덱스에서 멈추게 된다. 한편, R은 R에 위치한 원소가 9(=pivot) 보다 작거나 같은 값이 나올 때까지 리스트의 왼쪽 방향으로 움직인다. 하지만 시작 지점인 인덱스 9에서부터 pivot보다 작은 값이 발견되었기에 R은 움직이지 않은 채 다음 단계로 진행된다.

3. 동작 과정 (3)에 따라 L과 R이 교차하지 않았으므로 두 인덱스에 위치한 원소값을 교환한다. 이후, 다시 동작 과정 (2)를 진행한다.
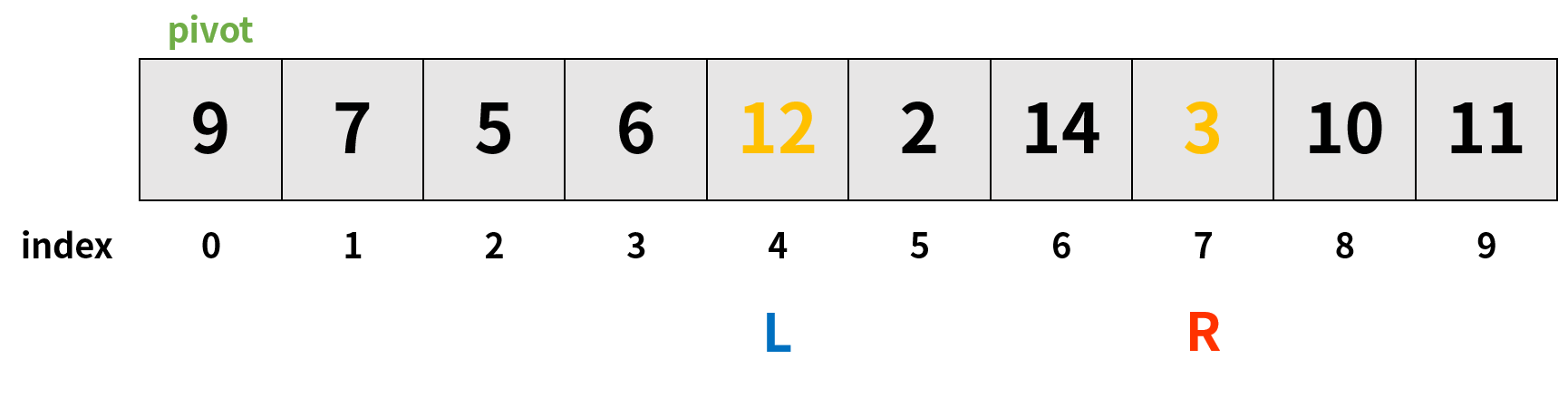
4. L은 pivot보다 큰 숫자를 바로 다음 인덱스에서 찾아버렸기 때문에 인덱스 4에서 멈추며, R은 인덱스 7에서 멈춘다.

5. 이번에도 L과 R이 교차하지 않았으므로 두 인덱스에 위치한 원소값을 교환한 후, 다시 동작 과정 (2)를 진행한다.
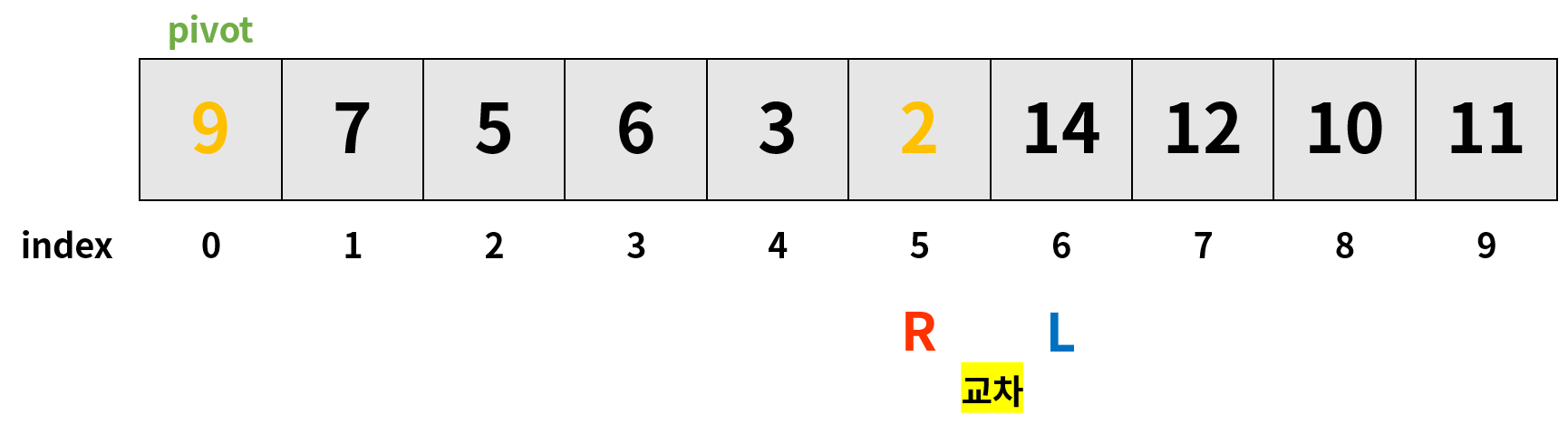
6. 동작 과정 (2)를 다시 진행한 결과, L과 R이 교차하였다. 동작 과정 (4)에 따라 pivot과 R에 위치한 원소값을 교환한다.

7. 교환 후 pivot의 위치는 인덱스 5 이다.

8. 이제 인덱스 5에 위치한 원소 '9'는 정렬된 것이라고 간주하며, 왼쪽과 오른쪽을 분할하여 부분집합을 만든다. 이후 왼쪽과 오른쪽 부분집합에 대해 퀵 정렬 알고리즘을 재귀 호출한다. 왼쪽 부분집합에 대해 먼저 재귀 호출했다고 가정하면 그다음 단계에서 바로 [2, 7, 5, 6, 3]이라는 리스트에 대해 퀵 정렬 알고리즘이 다시 진행된다.

9. 또다시 pivot은 해당 리스트의 가장 왼쪽 원소인 '2'로 지정되며, L은 해당 리스트의 가장 왼쪽 인덱스인 0, R은 해당 리스트의 가장 오른쪽 인덱스인 4로 지정된다.

10. 동작 과정 (2)를 진행한 결과 L은 바로 다음 인덱스인 1에서 멈췄지만, R은 2(=pivot) 보다 작은 숫자를 발견하지 못해 이동 가능한 최대 지점인 0번 인덱스까지 이동하였다.

11. L과 R이 교차했으므로 pivot과 R에 위치한 원소값을 교환해준다. 다만, 이 때는 pivot이 위치하는 인덱스와 R이 동일하므로 동일한 값이다. 즉, 교환의 의미가 없다.

12. 이제 0번 인덱스에 위치한 원소 '2' 또한 정렬된 것으로 간주하고 0번 인덱스를 기준으로 왼쪽 부분집합과 오른쪽 부분집합을 분할한다. 이후 왼쪽 부분집합과 오른쪽 부분집합에 대해 퀵 정렬 알고리즘을 재귀 호출한다. 다만, 왼쪽 부분집합은 공집합이라 재귀 호출의 탈출 조건에 만족되며 바로 무시된다. 이후 오른쪽 부분집합인 [7, 5, 6, 3]에 대해 퀵 정렬 알고리즘을 다시 수행할 것이다.
(더 이상의 설명은 생략!)
메모리 사용 공간
n개의 원소에 대하여 n개의 메모리 사용
연산 시간
1. 최선의 경우 (Best Case) : 왼쪽 부분집합과 오른쪽 부분집합이 정확히 이등분되는 경우
- 최선의 경우의 시간 복잡도 T(n) = O(N log N)
2. 최악의 경우 (Worst Case) : 부분집합이 1개와 n-1개로 치우쳐 분할되는 경우가 반복되는 경우
- 최악의 경우의 시간 복잡도 T(n) = O(N^2)
* 특이하게 거의 모든 사람들이 퀵 정렬의 시간 복잡도를 최악의 경우의 시간 복잡도가 아닌 평균적인 시간 복잡도로 설명하고 있다. 최악의 경우가 되려면 리스트가 오름차순 혹은 내림차순으로 정렬된 상태로 주어져야 하는데, 일반적인 상황에서 리스트가 정렬된 상태로 주어질 경우는 극히 드물기 때문이다. 수학적인 내용을 잘 정리해주신 분이 계신데 자세한 내용이 알고 싶다면 여기를 들어가서 확인해보자. 아무튼, '퀵 정렬의 시간 복잡도는 O(N log N)이다'라는 말은 엄밀히 말해서 Big-O Notation의 취지에 부합하지 않기 때문에 틀린 말이며, N log N으로 시간 복잡도를 표현하고 싶다면 세타(Theta) 표기법을 사용하여 θ(N log N)으로 표현하는 것이 더 올바르다. 그럼에도 불구하고 보편적으로 빅오(Big-O) 표기법을 많이 쓰니... 일단은 시간 복잡도를 그렇게 표현하도록 하겠다!
∴ 시간 복잡도 : O(N log N)
소스 코드
# 퀵 정렬 (Quick Sort)
# 퀵 정렬 - 오름차순 (Quick Sort - Ascending)
def partition_ASC(arr, start, end):
pivot = arr[start]
L = start
R = end
done = False
while not done:
while L <= len(arr)-1 and arr[L] <= pivot:
if L == len(arr)-1: # 리스트를 벗어나는 것을 방지
break
L += 1
while R >= 0 and pivot < arr[R]:
if R == 0: # 리스트를 벗어나는 것을 방지
break
R -= 1
if R <= L: # 교차했다면
done = True
else: # 교차하지 않았다면
arr[L], arr[R] = arr[R], arr[L]
arr[start], arr[R] = arr[R], arr[start]
return R # 새로운 pivot 위치 리턴
def quick_sort_ASC(arr, start, end):
if start < end:
pivot = partition_ASC(arr, start, end)
quick_sort_ASC(arr, start, pivot - 1)
quick_sort_ASC(arr, pivot + 1, end)
return arr
# 퀵 정렬 - 내림차순 (Quick Sort - Descending)
def partition_DESC(arr, start, end):
pivot = arr[start]
L = start
R = end
done = False
while not done:
while L <= len(arr)-1 and arr[L] >= pivot:
if L == len(arr)-1: # 리스트를 벗어나는 것을 방지
break
L += 1
while R >= 0 and pivot > arr[R]:
if R == 0: # 리스트를 벗어나는 것을 방지
break
R -= 1
if R <= L: # 교차했다면
done = True
else: # 교차하지 않았다면
arr[L], arr[R] = arr[R], arr[L]
arr[start], arr[R] = arr[R], arr[start]
return R # 새로운 pivot 위치 리턴
def quick_sort_DESC(arr, start, end):
if start < end:
pivot = partition_DESC(arr, start, end)
quick_sort_DESC(arr, start, pivot - 1)
quick_sort_DESC(arr, pivot + 1, end)
return arr
# 난수를 생성하여 test해보기 (Test by random number)
from random import randint
lst = [randint(1, 101) for i in range(8)]
print('Quick Sort(ASC) :', lst, end=' '); quickSort_ASC(lst, 0, len(lst)-1); print('->', lst)
# Quick Sort(ASC) : [80, 69, 21, 45, 58, 53, 16, 62] -> [16, 21, 45, 53, 58, 62, 69, 80]
lst = [randint(1, 101) for i in range(8)]
print('Quick Sort(DESC) :', lst, end=' '); quickSort_DESC(lst, 0, len(lst)-1); print('->', lst)
# Quick Sort(DESC) : [53, 49, 7, 28, 60, 44, 28, 101] -> [101, 60, 53, 49, 44, 28, 28, 7]
'Dev > 알고리즘' 카테고리의 다른 글
| [알고리즘][파이썬/Python] 병합 정렬 (Merge Sort) (0) | 2020.03.23 |
|---|---|
| [알고리즘][파이썬/Python] 쉘 정렬 (Shell Sort) (0) | 2020.03.22 |
| [알고리즘][파이썬/Python] 삽입 정렬 (Insertion Sort) (0) | 2020.03.21 |
| [알고리즘][파이썬/Python] 선택 정렬 (Selection Sort) (0) | 2020.03.20 |
| [알고리즘][파이썬/Python] 버블 정렬 (Bubble Sort) (0) | 2020.03.19 |
![[알고리즘][파이썬/Python] 퀵 정렬 (Quick Sort)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbv5SDy%2FbtqDvY5IRKq%2FAAAAAAAAAAAAAAAAAAAAAO0_mvRO4u8aRnIXWkZO86GyEMWHOPWZt9koEC6RUwRc%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D3rc0Lt2PB4JmnFaraDjXNW0CnBM%253D)