문제
시간 제한 : 0.5 초 (추가 시간 없음), 메모리 제한 : 4 MB
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 2 ³¹ 보다 작다.
입출력 예

제출 코드
n, k = map(int, input().split())
c = [int(input()) for i in range(n)] # 코인의 종류
dp = [0 for i in range(k+1)] # 사이즈 k+1만큼의 리스트 선언
dp[0] = 1 # 인덱스 0은 동전을 1개만 쓸 때의 경우의 수를 고려하기 위해 선언
for i in c:
for j in range(i, k+1):
if j-i >= 0:
dp[j] += dp[j-i]
print(dp[k])문제의 핵심
# 1
동적 계획법(Dynamic Programming, DP)은 최적화 문제를 해결하는 알고리즘으로서, 아래의 내용을 항상 명심해야 한다.
- '전체의 문제'를 '부분 문제'로 잘 나누었는가? 그렇다면 전체 문제를 해결하기 위한 부분 문제의 점화식은 무엇인가?
- 부분 문제들을 해결하며 얻는 결과값을 메모이제이션하는가?
- 부분 문제의 점화식은 부분 문제들 사이의 '관계'를 빠짐없이 고려하는가?
# 2
위 #1 을 바탕으로 했을 때 2293번의 문제 핵심은 다음과 같다.
- '가치의 합이 k원이 되는 경우의 수'를 구하는 전체의 문제를, '가치의 합이 i (1 ≤ i ≤ k)원이 되는 경우의 수'를 구하는 부분 문제로 나눈다. 추가적으로 부분 문제를 더욱 세부적으로 나눌 것인데, '특정 동전을 썼을 때 가치의 합이 i원이 되는 경우의 수'를 구하는 부분 문제로 나눈다.
- 위에서 언급한 부분 문제들을 해결해나가며 메모이제이션을 할 것인데, 시간 제한이 0.5초이며 메모리 제한도 4MB밖에 되지 않기 때문에 하나의 리스트 안에서 덮어 씌우는 식으로 빠르게 해결해나가야 한다.
- 입출력 예시로 주어진 경우 말고도 다른 예시를 생각해보며 테스팅해봐야 한다.
라인 별 풀이
(1) line 2
코인의 종류를 오름차순으로 정렬해야 할 줄 알았는데 정렬하지 않고 동작시켜도 문제가 없었다.
(2) line 3
합이 i원이 되는 경우의 수를 구하기 위해 리스트 dp에 0을 k+1개 초기화한다. dp[1]은 합이 1원이 되는 경우의 수, dp[2]는 합이 2원이 되는 경우의 수,... , dp[k]는 합이 k원이 되는 경우의 수이다.
(3) line 4
dp[0]은 위 논리에 따라 '합이 0원이 되는 경우의 수'가 아니다. 이건 아래에 더 자세히 기술하겠다.
(4) line 6
첫 번째 for문에서는 각 코인의 종류를 전부 순회한다. 입출력 예시의 경우, 1원 - 2원 - 5원 순으로 순회한다.
(5) line 7
dp를 순회하며 특정 가치를 가진 동전을 썼을 때 합이 j원이 되는 경우의 수가 있다면 리스트 dp에 기록하기 위한 for문이다. 만약 동전이 3원짜리라면 dp[1], dp[2]는 고려할 필요가 없으므로 dp[3]부터 순회한다.
(6) line 8, 9
이건 코드를 실행하는 과정을 캡처한 후 설명하는 것이 더 편할 것 같다.
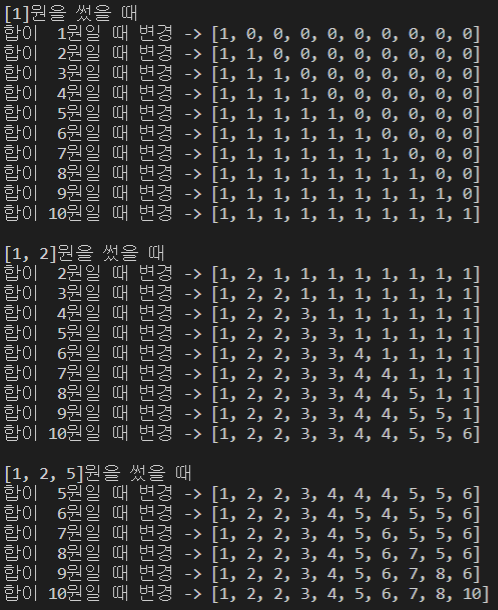
먼저 동전 1원일 때를 생각해보자 (i = 1). j는 i부터 시작하므로 가장 처음 나오는 j는 1이다. j - i는 1 - 1이므로 0과 같다. 조건문의 조건에 만족하므로 dp[1] = dp[1] + dp[0]이 된다. dp[1] = 0 + 1이 되는데, 이처럼 동전이 딱 하나만 쓰일 때 dp[0]에 할당해놓은 1을 이용한다. 이것이 line 4에서 설명하지 못한 부분이다. 계속 j가 늘어나도 조건문의 조건 'j - i >= 0'이 만족하므로 dp[j]에 dp[j] + dp[j-i] 값이 덮어 씌워진다.
문제는 2원짜리 동전부터다 (i = 2). j는 2부터 시작하며 j - i = 0이므로 조건문의 조건에 만족한다. 그에 따라 dp[2] = dp[2] + dp[0] = 1 + 1이 된다. 이것 또한 2원짜리 동전을 하나만 쓰는 경우를 추가하기 때문에 dp[0]에 할당된 1을 이용했다. dp[3]은 dp[3] + dp[1] 인데, 이 얘기는 '1원짜리 동전으로 3원의 합을 만든 경우의 수(1+1+1)' + '1원짜리 동전으로 1원의 합을 만든 경우에 2를 더해서 만든 경우의 수(1+2)'라는 것이다.
설명이 복잡해 보일 수 있는데, 이러한 과정을 5원짜리 동전까지 모두 마치면 다음과 같은 리스트가 완성된다. (눈이 너무 아파서 대충 했는데 오타가 있어도 이해해주시고 알고리즘의 흐름을 중점적으로 봐주셨으면 합니다.)
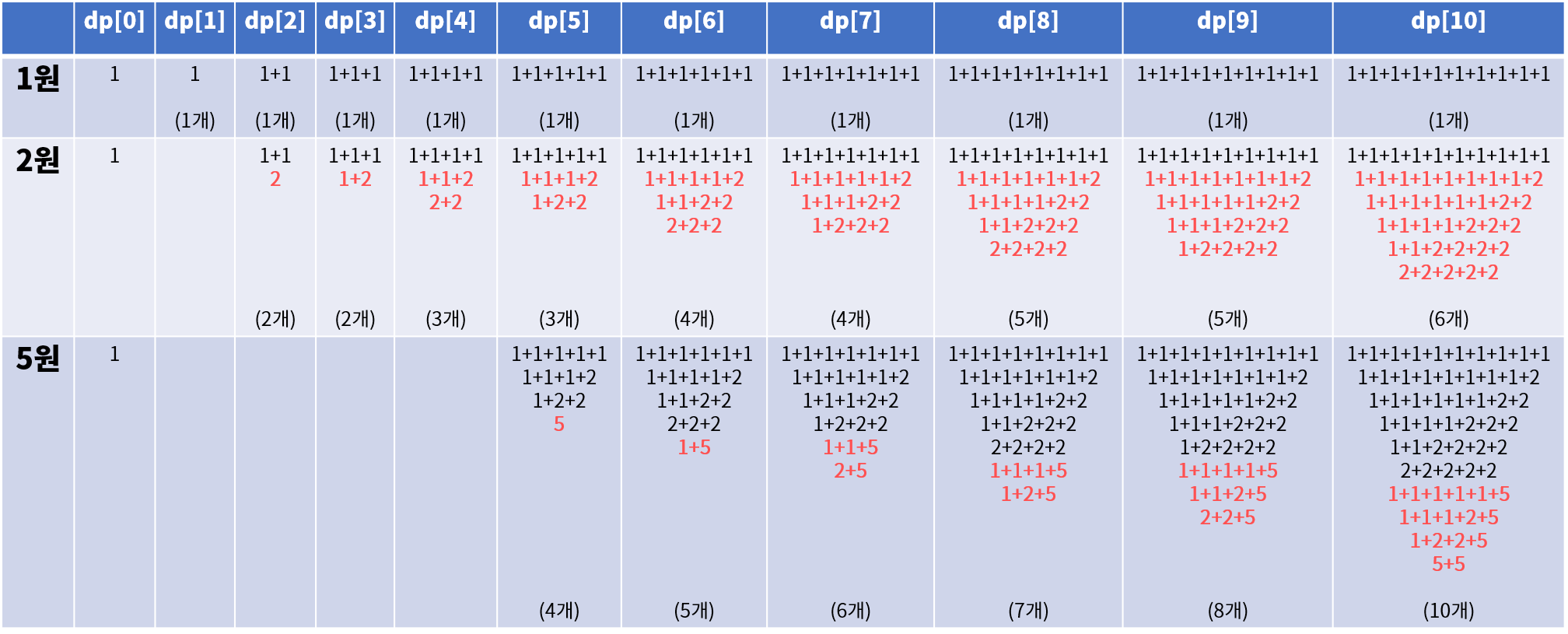
(7) line 10
합이 k원이 되는 경우의 수를 의미하는 dp[k]를 출력한다.
Source : https://www.acmicpc.net/problem/2293
'PS > 백준' 카테고리의 다른 글
| [백준 알고리즘][파이썬/Python] 1812번: 사탕 (0) | 2020.04.14 |
|---|---|
| [백준 알고리즘][파이썬/Python] 1094번: 막대기 (0) | 2020.04.13 |
| [백준 알고리즘][파이썬/Python] 1946번: 신입 사원 (3) | 2020.04.08 |
| [백준 알고리즘][파이썬/Python] 1541번: 잃어버린 괄호 (0) | 2020.04.07 |
| [백준 알고리즘][파이썬/Python] 10989번: 수 정렬하기 3 (0) | 2020.04.06 |
![[백준 알고리즘][파이썬/Python] 2293번: 동전 1](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FlB8EN%2FbtqDbFY4KI9%2F8m2v9HOpTwO34D55g687cK%2Fimg.png)